Summary
- Introduction
- Response curve
- Variable importance
- Evaluate models with independent data
- Saving a fitted_models object
Introduction
After the best performing models have been selected, users need to
fit this models (using fit_selected()) in order to explore
their characteristics and continue with the next steps. Fitted models
can then be used to assess variable importance in models, as well as to
explore variable response curves. We can also evaluate the selected
models using independent presence records that were not used during
model calibration.
To fit the selected models, we need a
calibration_results object. For more details in model
calibration, please refer to the vignette Model Calibration. The
calibration_results object generated in this vignette is
available as a data example in the package. Let’s load it.
#Load packages
library(kuenm2)
library(terra)
#> terra 1.8.60
#Import calib_results_maxnet
data("calib_results_maxnet", package = "kuenm2")
#Print calibration result
calib_results_maxnet
#> calibration_results object summary (maxnet)
#> =============================================================
#> Species: Myrcia hatschbachii
#> Number of candidate models: 300
#> - Models removed because they failed to fit: 0
#> - Models identified with concave curves: 39
#> - Model with concave curves not removed
#> - Models removed with non-significant values of pROC: 0
#> - Models removed with omission error > 10%: 165
#> - Models removed with delta AIC > 2: 133
#> Selected models: 2
#> - Up to 5 printed here:
#> ID
#> 192 192
#> 219 219
#> Formulas
#> 192 ~bio_1 + bio_7 + bio_15 + I(bio_1^2) + I(bio_7^2) + I(bio_15^2) -1
#> 219 ~bio_1 + bio_7 + bio_12 + bio_15 + I(bio_1^2) + I(bio_7^2) + I(bio_12^2) + I(bio_15^2) -1
#> Features R_multiplier pval_pROC_at_10.mean Omission_rate_at_10.mean
#> 192 lq 0.1 0 0.0769
#> 219 lq 0.1 0 0.0962
#> dAIC Parameters
#> 192 0.000000 6
#> 219 1.179293 7This object contains the results of candidate models calibrated using
the maxnet algorithm. The package also provides a similar
example using the glm algorithm, which works in exactly the
same way.
#Import calib_results_glm
data("calib_results_glm", package = "kuenm2")
#Print calibration result
calib_results_glm
#> calibration_results object summary (glm)
#> =============================================================
#> Species: Myrcia hatschbachii
#> Number of candidate models: 122
#> - Models removed because they failed to fit: 0
#> - Models identified with concave curves: 18
#> - Model with concave curves not removed
#> - Models removed with non-significant values of pROC: 0
#> - Models removed with omission error > 10%: 101
#> - Models removed with delta AIC > 2: 20
#> Selected models: 1
#> - Up to 5 printed here:
#> ID Formulas Features
#> 85 85 ~bio_1 + bio_7 + bio_12 + I(bio_1^2) + I(bio_7^2) + I(bio_12^2) lq
#> pval_pROC_at_10.mean Omission_rate_at_10.mean dAIC Parameters
#> 85 0 0.0904 0 6Note that the calibration_results object stores only the
information related to the calibration process and model evaluation—it
does not include the fitted maxnet (or glm)
models themselves.
To obtain the final fitted models, we need to use the
fit_selected() function. By default, this function fits a
full model (i.e., without partitions and without splitting the data into
training and testing sets). However, you can configure it to fit final
models with partitions if desired.
In this example, we’ll fit the final models using the same partition settings (4-fold cross-validation) as used in the Model Calibration vignette.
# Fit selected models using calibration results
fm <- fit_selected(calibration_results = calib_results_maxnet,
partition_method = "kfolds", n_partitions = 4)
# Fitting partitions...
# |========================================================================| 100%
# Fitting full models...
# |========================================================================| 100%The fit_selected() function returns a
fitted_models object, a list that contains essential
information from the fitted models, which is required for the subsequent
steps.
You can explore the contents of the fitted_models object
by indexing its elements. For example, the fitted maxnet
(or glm) model objects are stored within the
Models element. Note that Models is a nested
list: for each selected model (in this case, models 192 and 219), it
includes both the partitions (if fitted with partitions) and the full
model.
#See names of selected models
names(fm$Models)
#> [1] "Model_192" "Model_219"
#See models inside Model 192
names(fm$Models$Model_192)
#> [1] "Partition_1" "Partition_2" "Partition_3" "Partition_4" "Full_model"The fitted_models object also stores the thresholds that
can be used to binarize the models into suitable and unsuitable areas.
These thresholds correspond to the omission error used during model
selection (e.g., 5% or 10%).
You can access the omission error used to calculate the thresholds directly from the object:
#Get omission error used to select models and calculate the thesholds
fm$omission_rate
#> [1] 10The omission error used to calculate the thresholds was 10%, meaning that when the predictions are binarized, approximately 10% of the presence records used to calibrate the models will fall into cells with predicted values below the threshold.
The thresholds are summarized in two ways: the mean and median across partitions for each model, and the consensus mean and median across all selected models (when more than one model is selected):
fm$thresholds
#> $Model_192
#> $Model_192$mean
#> [1] 0.241469
#>
#> $Model_192$median
#> [1] 0.2535061
#>
#>
#> $Model_219
#> $Model_219$mean
#> [1] 0.2573623
#>
#> $Model_219$median
#> [1] 0.2597515
#>
#>
#> $consensus
#> $consensus$mean
#> [1] 0.2494156
#>
#> $consensus$median
#> [1] 0.2566288
#>
#>
#> $type
#> [1] "cloglog"Now, we can use the fitted_models object to generate
response curves and compute variable importance.
Response curve
The response curves illustrate how each environmental variable influences the predicted suitability, while keeping all other variables constant.
By default, the curves are generated with all other variables set to
their mean values (or the mode for categorical variables), calculated
from the combined set of presence and background localities
(averages_from = "pr_bg"). You can change this behavior to
use only the presence localities by setting
averages_from = "pr".
Let’s check which variables are available to plot by examining the coefficients of the full models:
#Get variables with non-zero coefficients in the models
fm$Models[[1]]$Full_model$betas #From the first model selected
#> bio_1 bio_7 bio_15 I(bio_1^2) I(bio_7^2) I(bio_15^2)
#> 11.572321659 0.215970079 0.369077970 -0.356605446 -0.020306099 -0.006200151
fm$Models[[2]]$Full_model$betas #From the second model selected
#> bio_1 bio_12 bio_15 I(bio_1^2) I(bio_7^2)
#> 1.178814e+01 1.638570e-02 3.406100e-01 -3.625405e-01 -1.440450e-02
#> I(bio_12^2) I(bio_15^2)
#> -5.261860e-06 -5.623987e-03The variables bio_1, bio_7,
bio_12 and bio_15have non-zero coefficient
values, which means they contribute to the model and are available for
generating response curves.
By default, response curves are computed using all selected models. The resulting plots include a line for the mean response, along with a shaded area representing the 95% confidence interval.
par(mfrow = c(2, 2)) #Set grid of plot
response_curve(models = fm, variable = "bio_1")
response_curve(models = fm, variable = "bio_7")
response_curve(models = fm, variable = "bio_12")
response_curve(models = fm, variable = "bio_15")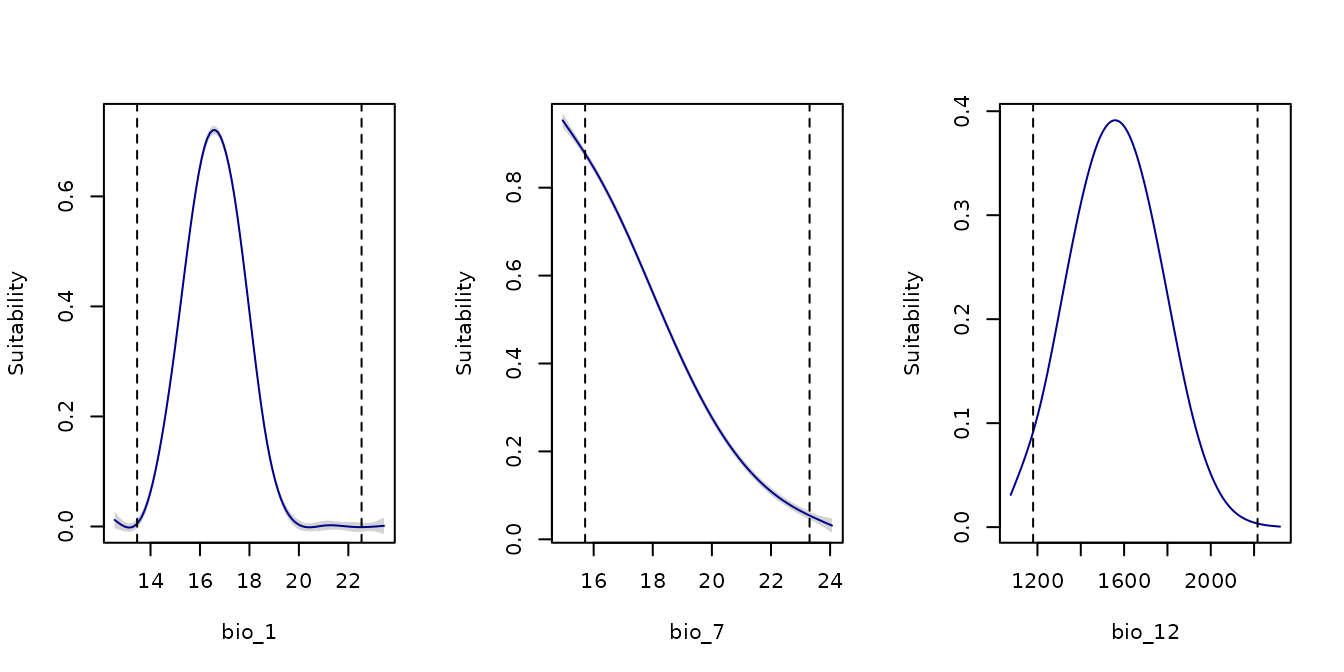
on.exit() #Reinitiate gridWe can also specify which of the selected models should be used to generate the response curves:
par(mfrow = c(2, 2)) #Set grid of plot
response_curve(models = fm, variable = "bio_1",
modelID = "Model_192", main = "Model_192")
response_curve(models = fm, variable = "bio_1",
modelID = "Model_219", main = "Model_219")
response_curve(models = fm, variable = "bio_7",
modelID = "Model_192", main = "Model_192")
response_curve(models = fm, variable = "bio_7",
modelID = "Model_219", main = "Model_219")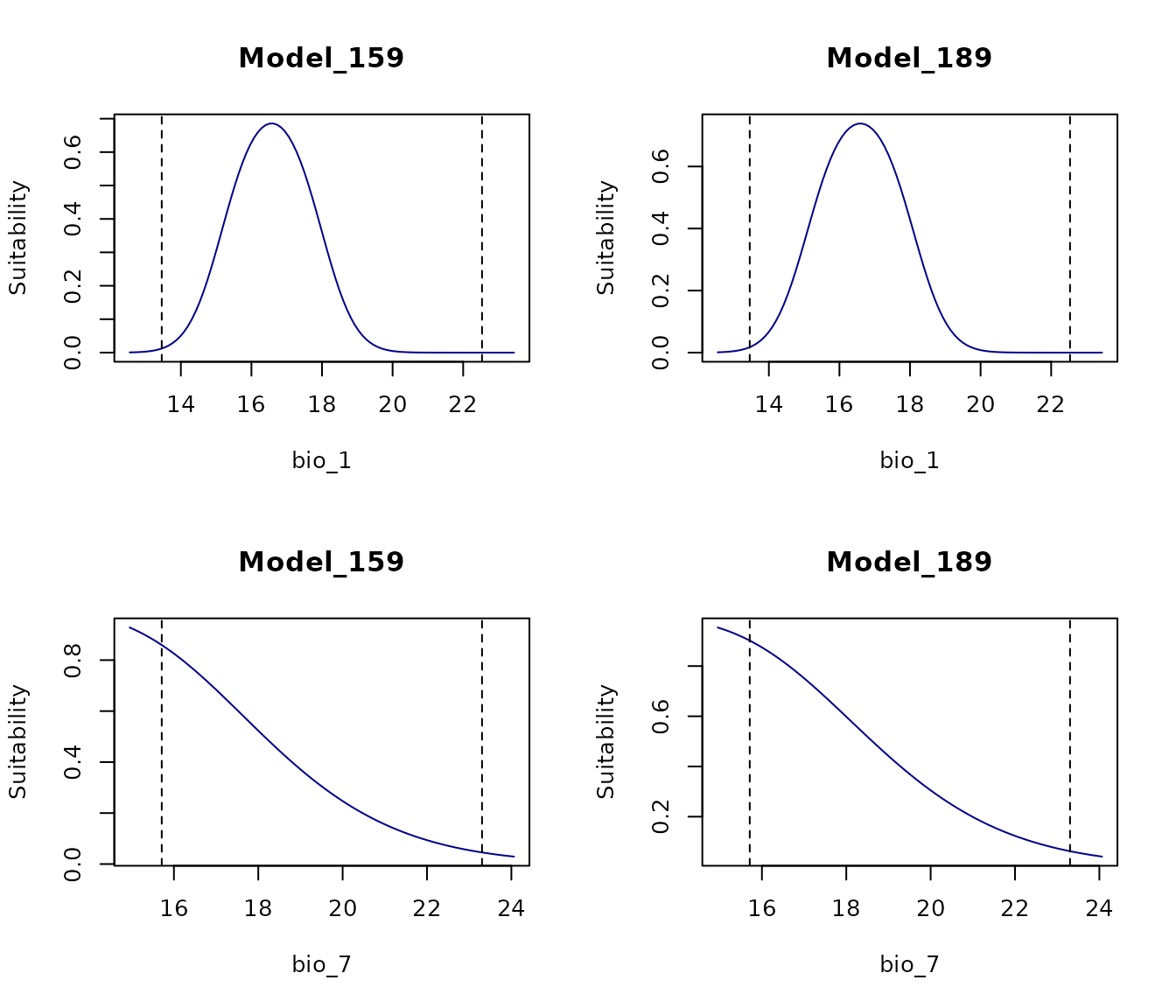
on.exit() #Reinitiate gridThe dashed lines indicate the range of the variable within the
calibration data. By default, the plot extends beyond these limits based
on the variable’s minimum and maximum values and the
extrapolation_factor (when
extrapolation = TRUE). The default extrapolation is set to
10% of the variable’s range (i.e., range × 0.1).
If extrapolation = FALSE, no extrapolation occurs, and
the plot limits match the calibration data range exactly.
We can increase the extrapolation factor to allow a broader range beyond the observed data. Below is the response curve plotted with an extrapolation factor of 2:
par(mfrow = c(2, 2)) #Set grid of plot
response_curve(models = fm, variable = "bio_1", extrapolation_factor = 2)
response_curve(models = fm, variable = "bio_7", extrapolation_factor = 2)
response_curve(models = fm, variable = "bio_12", extrapolation_factor = 2)
response_curve(models = fm, variable = "bio_15", extrapolation_factor = 2)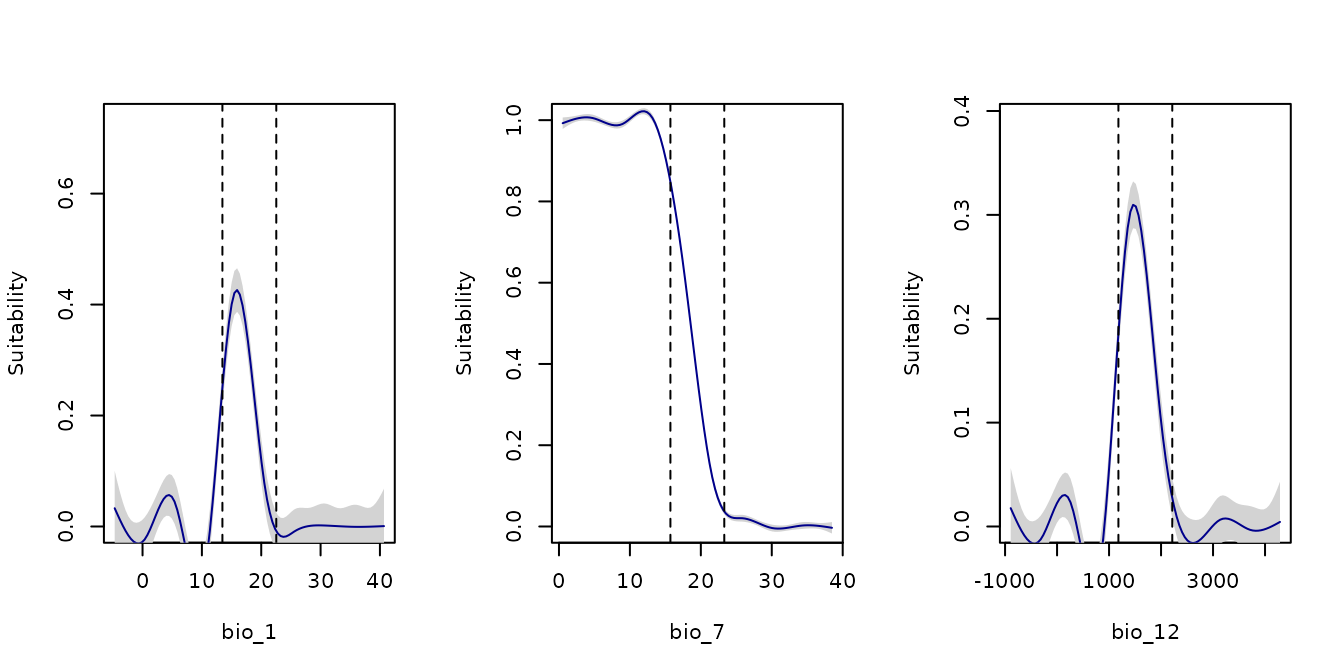
on.exit() #Reinitiate gridNote that the response curve now extends further beyond the observed data range (indicated by the dashed lines).
Optionally, we can manually set the lower and upper limits of the
variables. For example, since bio_12 represents annual
precipitation and negative values are not meaningful, we can set its
lower limit to 0:
response_curve(models = fm, variable = "bio_12",
extrapolation_factor = 0.1,
l_limit = 0)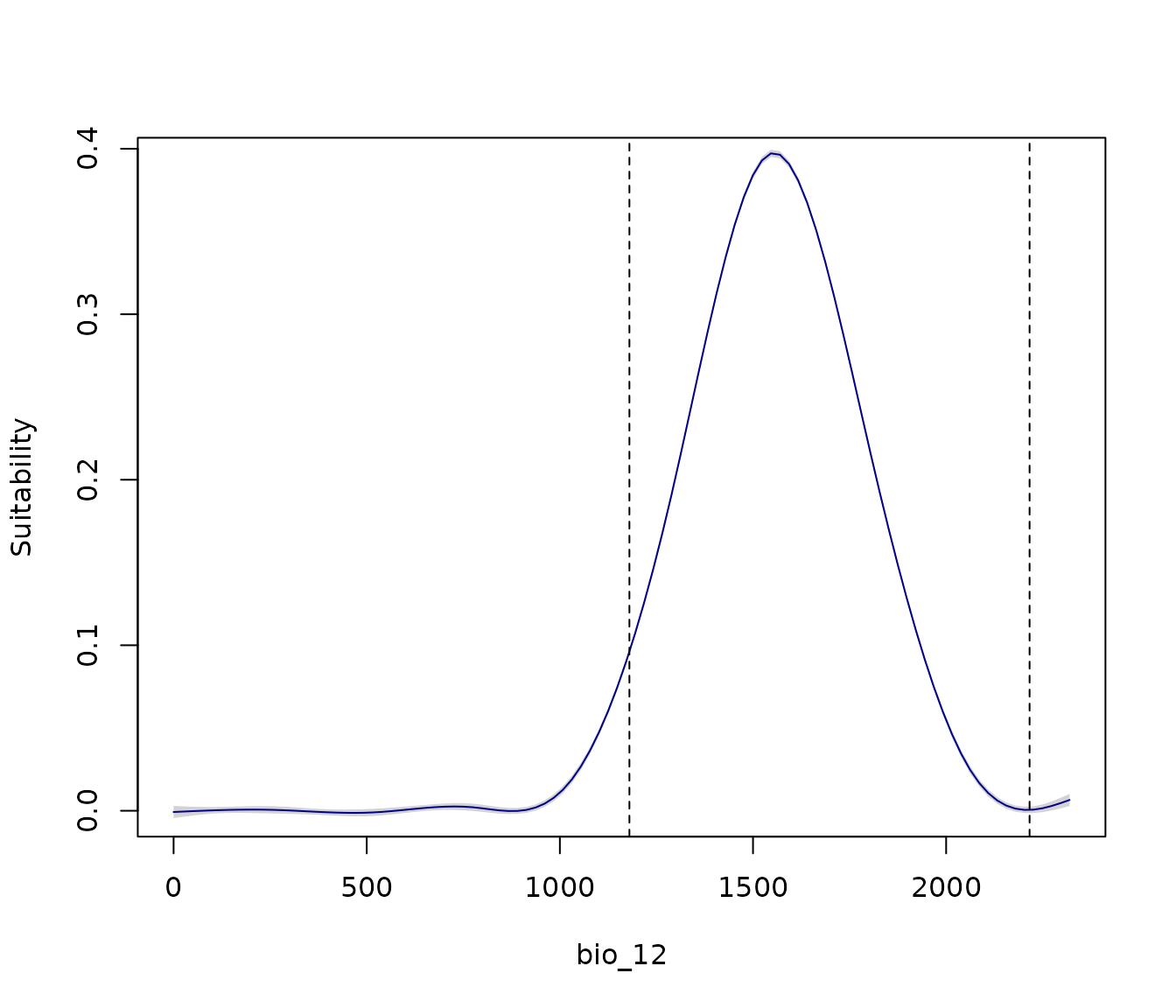
Now, the lower limit of the plot for bio_12 is set to 0.
Since we did not specify an upper limit, the plot uses the extrapolation
factor (here, 0.1) to define the upper limit.
Optionally, we can add the original presence and background points to
the plot by setting add_point = TRUE:
response_curve(models = fm, variable = "bio_1",
add_points = TRUE)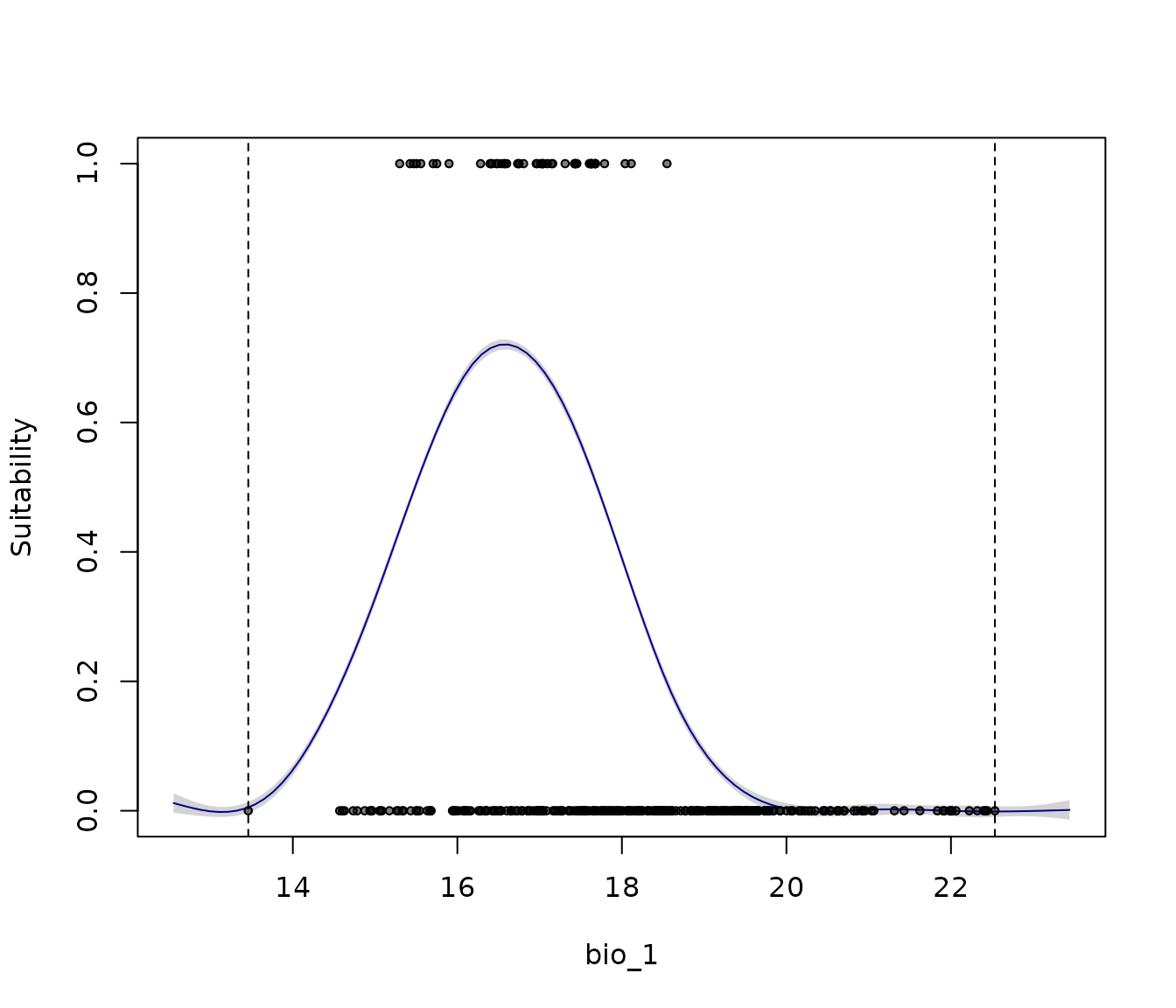
Variable importance
The relative importance of predictor variables can be calculated
using explained deviance through the var_importance()
function. This process starts by fitting the full model
(maxnet or glm), which includes all predictor
variables. Then, the function fits separate models excluding one
variable at a time, assessing how the removal affects model
performance.
By systematically evaluating the impact of each predictor’s exclusion, the function provides insights into the individual contribution of each variable to the model’s overall performance and explanatory power.
By default, the function runs on a single core. You can enable
parallel processing by setting parallel = TRUE and
specifying the number of cores with ncores. Note that
parallelization only speeds up the computation when there are many
variables (more than 7) and a large calibration dataset (over 15,000
presence and background points).
By default, variable importance is computed for all selected models:
# Calculate variable importance
imp <- variable_importance(models = fm)
# Calculating variable contribution for model 1 of 2
# |======================================================================| 100%
# Calculating variable contribution for model 2 of 2
# |======================================================================| 100%The function returns a data.frame with the relative
contribution of each variable. If multiple models are included in the
fitted object, an additional column identifies each
distinct model.
imp
#> predictor contribution Models
#> 1 I(bio_1^2) 0.330546900 Model_192
#> 2 bio_1 0.295001412 Model_192
#> 3 bio_15 0.209668355 Model_192
#> 4 I(bio_15^2) 0.156926301 Model_192
#> 5 I(bio_7^2) 0.006279520 Model_192
#> 6 bio_7 0.001577512 Model_192
#> 7 I(bio_1^2) 0.368476226 Model_219
#> 8 bio_1 0.332782286 Model_219
#> 9 bio_15 0.155708606 Model_219
#> 10 I(bio_15^2) 0.095186390 Model_219
#> 11 I(bio_12^2) 0.022722557 Model_219
#> 12 bio_12 0.021793617 Model_219
#> 13 I(bio_7^2) 0.003330318 Model_219We can visualize variable importance using the
plot_importance() function. When the
fitted_models object contains more than one selected model,
the plot displays a boxplot of contributions, along with the mean
contribution and the number (N) of fitted models.
plot_importance(imp)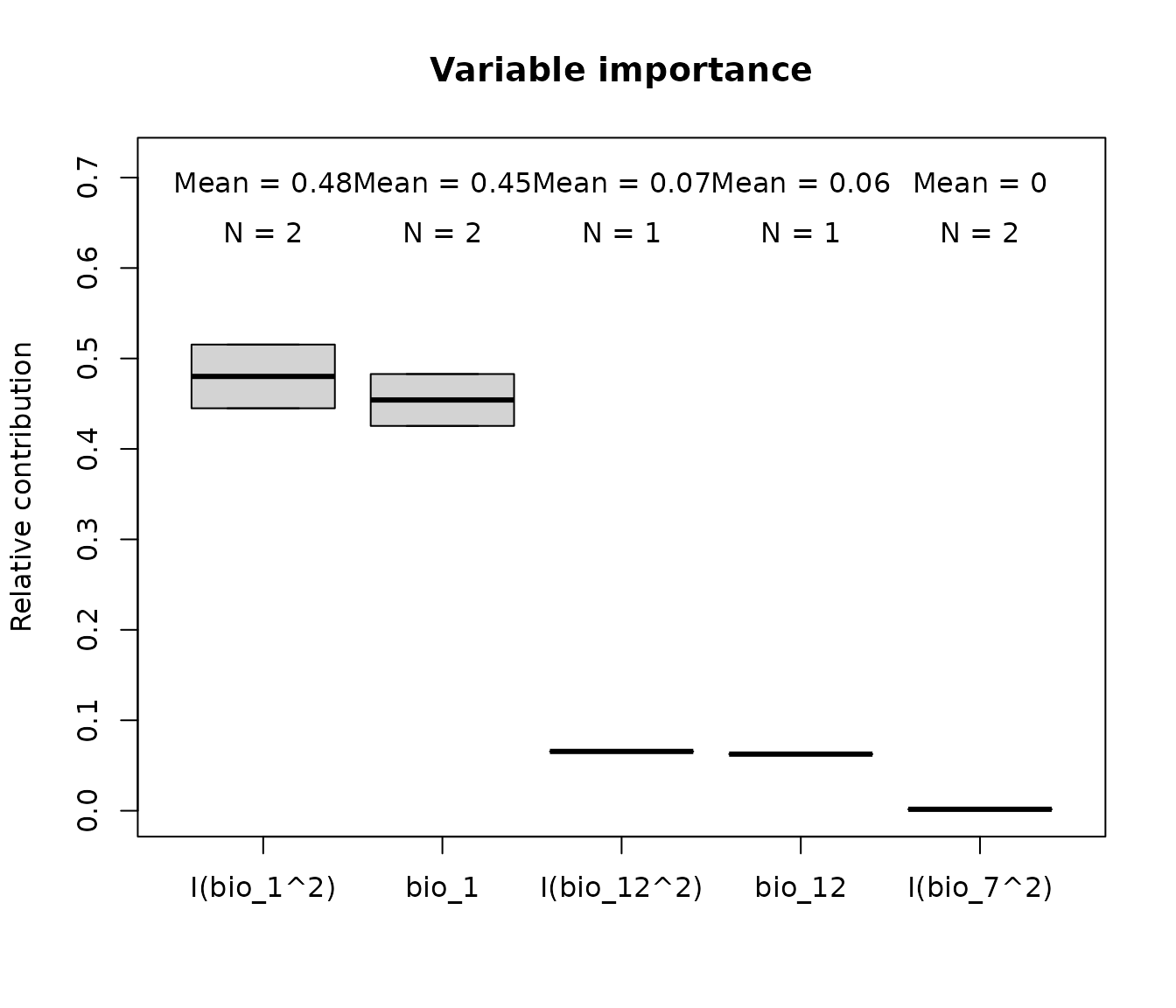
If variable importance is computed for a single model, the plot displays a barplot instead of a boxplot:
# Calculate variable importance for a specific selected Model
imp_192<- variable_importance(models = fm, modelID = "Model_192",
progress_bar = FALSE)
#Plot variable contribution for model 192
plot_importance(imp_192, main = "Variable importance - Model 192")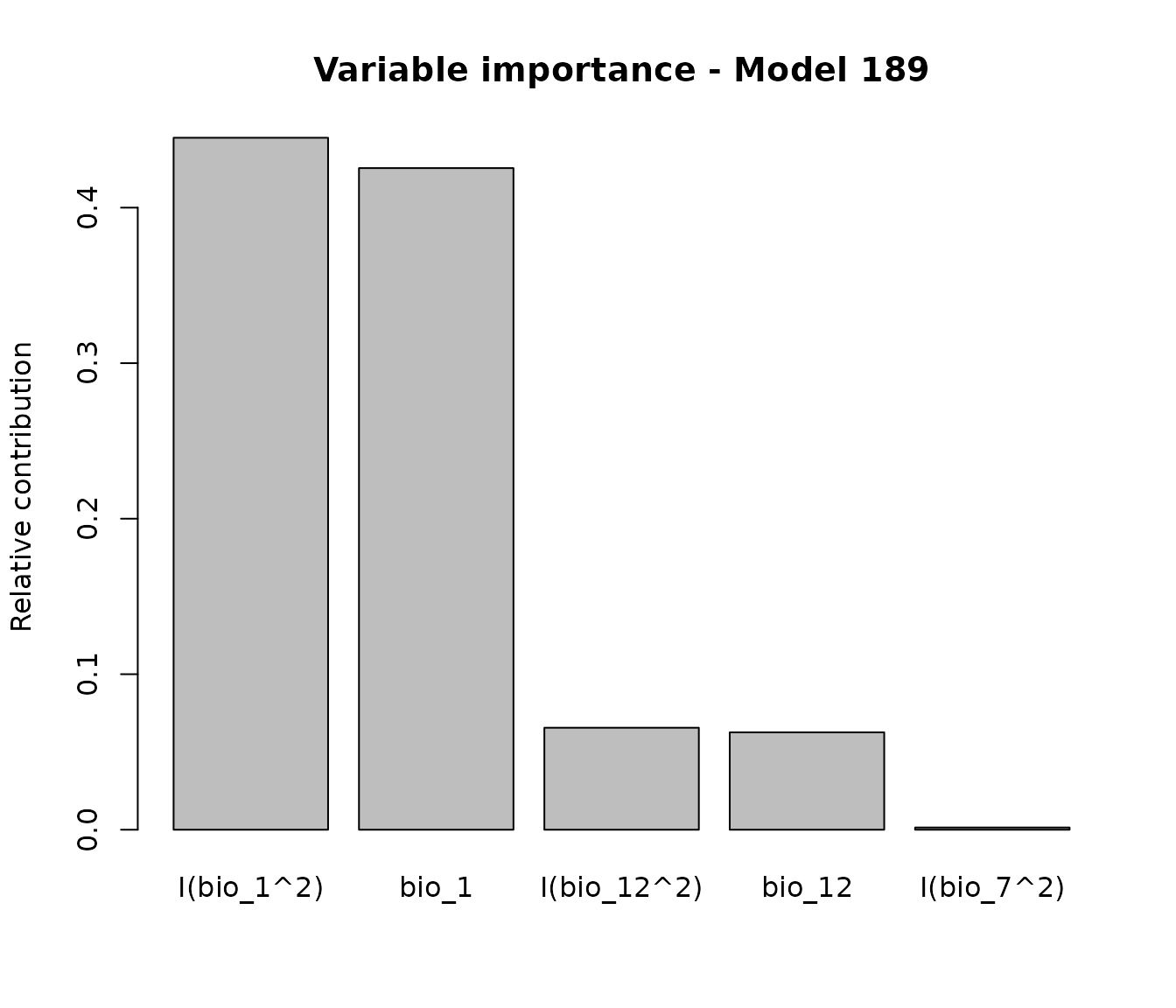
Evaluate models with independent data
We can evaluate the selected models using an independent set of presence records that were not used during model calibration. This approach is especially useful when new records become available or when working with invasive species. In the latter case, models are first calibrated using presence data from the native area and subsequently evaluated with data from the invaded area.
The independent_evaluation() function computes the
omission rate - i.e., the proportion of independent records that fall in
unsuitable areas, where “unsuitable” is defined according to the
omission threshold used during model calibration and selection (e.g.,
10%) - as well as the partial ROC. It also assesses whether the
environmental conditions in the independent data are analogous (i.e.,
within the range) to those in the calibration data.
As example of independent data, let’s use the new_occ
data example provided in the package. It contains coordinates of the
Myrcia hatschbachii sourced from NeotropicTree (Oliveira-Filho, 2017), and they
were not part of the occ_dataused to train the models.
# Import independent records
data("new_occ", package = "kuenm2")
# See data structure
str(new_occ)
#> Classes 'data.table' and 'data.frame': 82 obs. of 3 variables:
#> $ species: chr "Myrcia hatschbachii" "Myrcia hatschbachii" "Myrcia hatschbachii" "Myrcia hatschbachii" ...
#> $ x : num -48.3 -49.1 -49.9 -49.4 -49.9 ...
#> $ y : num -25.2 -25 -24.5 -24.5 -24.8 ...
#> - attr(*, ".internal.selfref")=<externalptr>For predicting the model to this new set of occurrence records, we
need to extract the environmental conditions on this locals. Let’s
import the variables we used to fit the models and extract to the
new_occ conditions:
# Import raster layers
var <- terra::rast(system.file("extdata", "Current_variables.tif",
package = "kuenm2"))
# Extract variables to occurrences
new_data <- extract_occurrence_variables(occ = new_occ, x = "x", y = "y",
raster_variables = var)
# See data structure
str(new_data)
#> 'data.frame': 82 obs. of 8 variables:
#> $ pr_bg : num 1 1 1 1 1 1 1 1 1 1 ...
#> $ x : num -48.3 -49.1 -49.9 -49.4 -49.9 ...
#> $ y : num -25.2 -25 -24.5 -24.5 -24.8 ...
#> $ bio_1 : num 20.2 18 16.6 17.8 16.7 ...
#> $ bio_7 : num 16.7 18.2 19.9 19.4 20.1 ...
#> $ bio_12 : num 2015 1456 1526 1414 1578 ...
#> $ bio_15 : num 43.8 33.7 29.1 32.2 26.5 ...
#> $ SoilType: num 6 6 6 6 6 10 10 10 10 10 ...Especially when using independent records that fall outside the calibration area (e.g., in an invaded region on another continent), it is common for the environmental conditions in these new records to be non-analogous (i.e., outside the range) to those in the calibration data.
To better illustrate this case, let’s add three fake records, in which some variables have non-analogous values, either higher than the upper limit or lower than the lower limit observed in the calibration data.
#Add some fake data beyond the limits of calibration ranges
fake_data <- data.frame("pr_bg" = c(1, 1, 1),
"x" = c(NA, NA, NA),
"y" = c(NA, NA, NA),
"bio_1" = c(10, 15, 23),
"bio_7" = c(12, 16, 20),
"bio_12" = c(2300, 2000, 1000),
"bio_15" = c(30, 40, 50),
"SoilType" = c(1, 1, 1))
# Bind data
new_data <- rbind(new_data, fake_data)Now, let’s evaluate this independent dataset (keep in mind that the last three records are fake):
# Evaluate models with independent data
res_ind <- independent_evaluation(fitted_models = fitted_model_maxnet,
new_data = new_data)The output is a list with three elements. The first one, evaluation, presents the evaluation metrics (omission rate and pROC) for each selected model, as well as for the overall consensus. We can see that all selected models have significant pROC values, but show higher omission rates (around 40% of the independent records fall in areas predicted as unsuitable) compared to the threshold specified during model calibration (10%).
res_ind$evaluation
#> Model consensus Omission_rate_at_10 Mean_AUC_ratio pval_pROC
#> 1 Model_192 mean 0.4352941 1.166789 0
#> 2 Model_192 median 0.4000000 1.139045 0
#> 3 Model_219 mean 0.4235294 1.190714 0
#> 4 Model_219 median 0.4000000 1.138885 0
#> 5 General_consensus median 0.4000000 1.136853 0
#> 6 General_consensus mean 0.4352941 1.180920 0When perform_mop is set to TRUE, the
function also returns the mop_results, which is a list
containing the output of mop::mop() function. The main
results of the MOP analysis are appended to the
predictions element of the list.
For each records, the following information is provided:
- mop_distance: the distance (i.e., dissimilarity) between the environmental conditions in calibration data and those at the location of the independent record.
- inside_range: wheter the environmental conditions at the location of the independent record fall within the calibration range.
- n_var_out: the number of variables at the location of the independent record that are non-analogous (i.e., fall outside the calibration range).
- towards_low: the names of variables with values lower than the minimum observed in the calibration data.
- towards_high: the names of variables with values higher than the maximum observed in the calibration data.
# Show the mop results for the last 5 independent records
res_ind$predictions$continuous[81:85 ,c("mop_distance", "inside_range", "n_var_out",
"towards_low", "towards_high")]
#> mop_distance inside_range n_var_out towards_low towards_high
#> 81 7.753558 TRUE 0 <NA> <NA>
#> 82 6.622770 TRUE 0 <NA> <NA>
#> 83 157.782905 FALSE 3 bio_7, bio_1 bio_12
#> 84 21.045482 TRUE 0 <NA> <NA>
#> 85 183.905420 FALSE 2 bio_12 bio_1Note that two of the three fake records we added to
new_data have non-analogous environmental conditions. One
of them falls in a location where bio_7 and bio_1 have
values lower than the minimum observed in the calibration data, while
bio_12 has a value higher than the maximum. Another record is
in a location where bio_12 is below the calibration range, and
bio_1 exceeds the upper limit.
When we setreturn_predictions = TRUE, the function also
returns the continuous predictions for each selected model and for the
general consensus:
# Show the continuous predictions for the last 5 independent records
# Round to two decimal places
round(res_ind$predictions$continuous[81:85, 1:6], 2)
#> Model_192.mean Model_192.median Model_219.mean Model_219.median
#> 81 0.57 0.63 0.58 0.65
#> 82 0.54 0.60 0.55 0.62
#> 83 1.00 1.00 0.96 1.00
#> 84 1.00 1.00 1.00 1.00
#> 85 0.00 0.00 0.00 0.00
#> General_consensus.median General_consensus.mean
#> 81 0.63 0.58
#> 82 0.61 0.54
#> 83 1.00 0.98
#> 84 1.00 1.00
#> 85 0.00 0.00If we set return_binary = TRUE, the function also
returns the binary predictions, with values classified as suitable (1)
or unsuitable (0), based on the threshold calculated using the omission
rate applied during model evaluation and selection:
# Show the continuous predictions for the last 5 independent records
res_ind$predictions$binary[81:85, 1:6]
#> Model_192.mean Model_192.median Model_219.mean Model_219.median
#> 81 1 1 1 1
#> 82 1 1 1 1
#> 83 1 1 1 1
#> 84 1 1 1 1
#> 85 0 0 0 0
#> General_consensus.mean General_consensus.median
#> 81 1 1
#> 82 1 1
#> 83 1 1
#> 84 1 1
#> 85 0 0These results help determine whether the independent data should be incorporated into the calibration dataset to re-run the models. If omission rates for the independent records are too high, pROC values are non-significant, or most of the records fall in locations with non-analogous environmental conditions, this suggests it may be a good idea to re-run the models, including the independent data this time.
Saving a fitted_models object
After fitting the best-performing models with
fit_selected(), we can proceed to predict the models for
single or multiple scenarios. As this object is essentially a list,
users can save it to a local directory using saveRDS().
Saving the object facilitates loading it back into your R session later
using readRDS(). See an example below: